Simulateur d'évolution d'épidémie de Virus, Covid-19 ou autre, via un modèle compartimental

Voir les chiffres réels en Polynésie Française

Ce simulateur montre une progression selon un modèle SIR étendu (Sain / Exposé / Infecté / Guéri (Recovered) / Hospitalisé / Décédé). Vous pouvez faire varier les paramètres sous le simulateur et modifier manuellement la courbe R₀ directement sur le graph (pour simuler des vagues de confinement/déconfinement par exemple). A et C représente respectivement l'arrêt d'import des cas et la mise en place du confinement. Tout échange et tout retour de terrain (notamment en Polynésie Française) sur la paramétrisation du modèle seront les bienvenus.
Par défaut, le 1er jour du graph est à 100 cas infectés (+50 exposés). Ceci correspond pour la Polynésie au 15 août. On peut bien sûr modifier cela.
Par défaut également, la série R est initialisée avec les valeurs communiquées jusqu'au 22/11/2020 en PF et ensuite R prend une valeur constante à 1.15 (hypothèse optimiste avec toutes mesures inchangées).
Enfin, vous pouvez modifier R(t) sur toute la série. Pour ce faire, afficher R0 et vous pourrez modifier par drag and drop sur chaque point (fastidieux et un export, modification puis import est peut être plus simple). Attention, si vous changez la largeur temporelle du graph, il faudra recommencer, il est donc conseillé d'exporter R(t) si vous l'avez modifiée...

Vous pouvez modifier les paramètres dans chaque groupe ci-dessous :

Relancer le graph (après changement de la courbe R₀)

Paramètres liés à la population et à la contagion

Population : 280000

Nombre initial d'infectés : 100

Durée infectieuse en jours : 5

Durée d'incubation en jours : 4

Durée d'incubation infectieuse en jours : 2

Taux de contagiosité en incubation E₂ (α) : 50

Paramètres liés à R₀

R0 sans confinement : 1.4

Durée avant confinement en jours : 5

R0 avec confinement : 1.4

Durée avant déconfinement en jours (à partir du début) : 45

R0 après déconfinement : 1.4

Durée de changement de R0 après (dé)confinement en jours : 15

Forcer R₀ :

Forcer R₀ même si la courbe a été modifiée

On considère que R₀ passe d'une valeur à une autre selon une fonction linéaire.

Paramètres liés aux suites cliniques

Attention, les pourcentages sont proportions du total d'exposés et non d'un total inférieur (les symptomatiques par exemple).

Durée avant hospitalisation en jours : 5.5

Taux d'hospitalisations moyennes (μ): 5%

Durée d'hospitalisation avant rétablissement en jours : 5

Taux de décès en hopital, hors réa (ω): 14%

Durée avant décès en hopital en jours, hors réa : 11

Taux de décès hors hopital (ε) : 0.4%

Durée avant décès hors hopital en jours : 11

Taux d'hospitalisations sévères (ν) : 1%

Durée d'hospitalisations sévères (réanimation) : 11.9

Taux de décès lors d'hospitalisations sévères (φ) : 30%

Paramètres techniques

Date début :

Durée du graph (jours) : 400

Capacité hospitalière : 185

Capacité en réanimation : 45

Type de graph :

Détaillé

Simple

Ecrétage :

Activer l'écrétage

Afficher capacités :

Afficher capacités hospitalières

Pourcentage de symptomatiques : 80%

Activer Réinfection :

Activer Réinfection

Durée de la mémoire immunitaire (jours) : 180

Les symptomatiques sont une proportion des porteurs P (P = E + I + H + D + R). Cette population est figurée pour comparaison aux dépistages (selon la stratégie de dépistage).

Import - Export des paramètres

Vous pouvez exporter les paramètres pour les importer plus tard, c'est utile si vous faites plusieurs simulations. Vous pouvez également modifier les paramètres avant de réimporter, il est possible de réimporter seulement quelques paramètres. Le format est JSON, le plus simple est que vous fassiez un premier export pour voir à quoi cela ressemble.

Exporter les paramètres

Importer les paramètres

Vous pouvez exporter également la fonction R₀(t).

Exporter R₀

Importer R₀

Aspects techniques

Schémas de principe

Schématiquement, les compartiments se présentent comme suit :

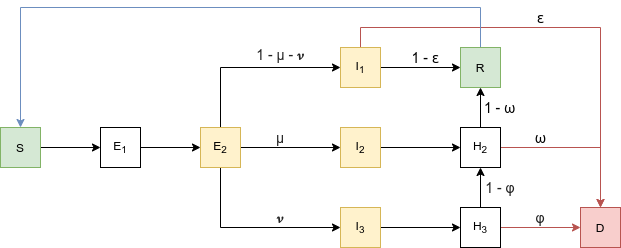
Schéma de principe du modèle à compartiments pour COVID-19

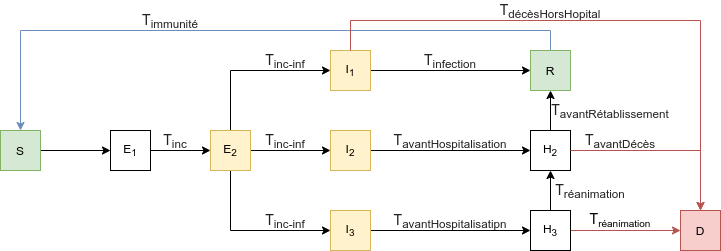
Schéma de principe du modèle à compartiments pour COVID-19 : Timings

Les différents niveaux de soins sont représentés par H₂ et H₃, la différenciation se fait en amont (I₁, I₂, I₃) afin d'avoir une différentation des durées (si besoin) et de pouvoir appliquer des statistiques connues.

Dans les paramètres d'initialisations, on prend comme hypothèse I₁(0) = Nombre d'infectés initiaux, et E(0) = 0.5 * I₁(0)

Définitions

Sain (S) : personne saine ne portant pas le virus

Exposé (E) : personne portant le virus en incubation, à ce stade la personne ne présente pas les symptomes mais peut être contagieuse (il faudrait ajouter un état pour le prendre en compte sans changer la période infectieuse)

Infecté (I) : personne portant le virus et présentant les symptômes, avec 3 niveaux 1 étant le moins grave

Hospitalisé (H) : personne hospitalisée, avec 2 niveaux 2 étant le moins grave

R₀ : nombre de personnes contaminées par un malade contagieux

β_Etat : taux de transmission de la maladie dans cet état

T_Incubation : Durée pendant laquelle une personne est infectée mais encore non contagieuse

T_Infectieux : Durée pendant laquelle une personne est contagieuse

T_{AvantHospitalisation} : Durée avant qu'une personne ne soit hospitalisée

T_{AvantRetablissement} : Durée pendant laquelle une personne est hospitalisée avant d'être guérie

T_Reanimation : Durée pendant laquelle une personne est hospitalisée en réa avant de décéder

T_{DecesEnHopital} : Durée pendant laquelle une personne est hospitalisée hors réa avant de décéder

T_{DecesHorsHopital} : Durée avant décès pour les décès hors hopital

T_Immunité : Durée pendant laquelle on est immunisé après une infection

Jeu d'équations utilisées

NB : on utilise les populations normalisées et I désigne par exemple la proportion de personnes infectées dans la population totale.

dS(i) / dt

= - S(i-1) * (β_I1 * I₁(i-1) + β_I2 * I₂(i-1) + β_I3 * I₃(i-1)) - β_E * S(i-1) * E₂(i-1) +

R(i-1) / T_Immunité

dE₁(i) / dt

= S(i-1) * (β_I1 * I₁(i-1) + β_I2 * I₂(i-1) + β_I3 * I₃(i-1)) + β_E * S(i-1) * E₂(i-1) -

E₁(i-1) / T_Inc

dE₂(i) / dt

E₁(i-1) / T_Inc

E₂(i-1) / T_Inc-inf

dI₁(i) / dt

(1- μ - ν) * E₂(i-1) / T_Inc-inf

(1- ε) * I₁(i-1) / T_Contagion

ε * I₁(i-1) / T_{DecesHorsHopital}

dI₂(i) / dt

μ * E₂(i-1) / T_Inc-inf

I₂(i-1) / T_{AvantHospitalisation}

dI₃(i) / dt

ν * E₂(i-1) / T_Inc-inf

I₃(i-1) / T_{AvantHospitalisation}

dH₂(i) / dt

I₂(i-1) / T_{AvantHospitalisation}

+ (1 - φ) *

H₃(i-1) / T_Reanimation

(1 - ω) * H₂(i-1) / T_{Retablissement}

ω * H₂(i-1) / T_{DecesEnHopital}

dH₃(i) / dt

I₃(i-1) / T_{AvantHospitalisation}

H₃(i-1) / T_Reanimation

dR(i) / dt

I₁(i-1) / T_Contagion

(1 - ω) * H₂(i-1) / T_{Retablissement}

R(i-1) / T_Immunité

dD(i) / dt

φ * H₃(i-1) / T_Reanimation

ε * I₁(i-1) / T_{DecesHorsHopital}

ω * H₂(i-1) / T_{DecesEnHopital}

R₀ et taux de transmission

Dans un modèle SIR simple, on peut écrire :

β =

R₀ / T_Contagion

Dans le présent modèle, on aura :

R₀ = Σ( β_e * p(e) * T_e)

où β_e est le taux de transmission dans un état infectieux e, p(e) la probabilité de cet état et T_e la durée de cet état. On utilise en outre un seul taux β représentant le taux de transmission dans l'état I₁ et des coefficients α_e pour ajuster les autres taux. Ainsi exprimé, on aura :

β =

R₀ / T_Contagion * ((1-μ-ν) + μ * α_I2 + ν * α_I3) + T_Inc-inf * α_E2

Initialisation des paramètres (cas du Covid-19/SARS-CoV-2)

Littérature

Les valeurs ne sont pas établies aujourd'hui avec certitudes et la littérature récente donne plusieurs valeurs pour les différentes caractéristiques de la maladie. En voici qui ont servi ici :

Source	Paramètre	Valeur
https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-Europe-estimates-and-NPI-impact-30-03-2020.pdf	R₀	3.87 (sans confinement) / 1.43 (avec confinement)
https://wwwnc.cdc.gov/eid/article/26/7/20-0282_article	R₀	5.7
https://wwwnc.cdc.gov/eid/article/26/7/20-0282_article (table 5)	T_Contagion	9 jours
https://wwwnc.cdc.gov/eid/article/26/7/20-0282_article	T_Incubation	5.2 jours
https://wwwnc.cdc.gov/eid/article/26/7/20-0282_article	T_{AvantHospitalisation}	5.5 jours (hors épidémie surveillée) / 1.5 jours (en épidémie surveillée)
https://wwwnc.cdc.gov/eid/article/26/7/20-0282_article	T_{AvantRétablissement}	11.5 jours
https://wwwnc.cdc.gov/eid/article/26/7/20-0282_article	T_Réanimation	11.2 jours (avant décès)
https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(20)30566-3/fulltext	T_Contagion	20 jours
https://annals.org/aim/fullarticle/2762808/incubation-period-coronavirus-disease-2019-covid-19-from-publicly-reported?searchresult=1	T_Incubation	5.1 jours

Fitting

Une fois les valeurs préssentie assignée, il convient de modifier certains paramètres dépendant de la population ou des équipements sanitaires : R₀ ainsi que les paramètres de suites cliniques.

Idéalement, il faudrait appliquer une minimisation des écarts sur une série de données connue.

Limitations, améliorations

Par défaut, on fait l'hypothèse que les patients guéris sont immunisés mais vous pouvez activer une immunité temporaire dans les paramètres techniques.

On ne tient pas compte de la capacité de charge hostpitalière, on peut imaginer que le taux de décès soit une fonction de celle ci, et introduire une transition H2 vers H3 dépendant de la capacité hospitalière également.

Une propagation 2D pourrait être représentée par ce modèle en considérant des compartiments par zones géographiques (pour les I et E essentiellement) et des paramètres par zone, tenant compte de la densité de population notamment, ainsi que des flux d'échanges.

De la même façon, une décomposition en compartiments d'âge serait possible, moins pour visualiser les effets par tranche d'âge que pour mieux modéliser les transmissions. Il faudrait revoir les équations pour généraliser en utilisant des matrices.

Hypothèse de population constante : on ne tient pas compte de la mortalité naturelle ni de la natalité ni des migrations de population entre le système et l'extérieur. Si on voulait en tenir compte (sur une période longue), il suffirait d'ajouter des taux à S et D, en admettant que les entrants sont sains.

Références

Pour le principe

Fondation de la théorie des modèles à compartiments : https://royalsocietypublishing.org/doi/pdf/10.1098/rspa.1927.0118
https://interstices.info/modeliser-la-propagation-dune-epidemie/
https://fr.wikipedia.org/wiki/Mod%C3%A8les_compartimentaux_en_%C3%A9pid%C3%A9miologie
http://www.math.ens.fr/enseignement/telecharger_fichier.php?fichier=1693
http://marcchoisy.free.fr/pdf/DeBoeck2010.pdf
https://www.theses.fr/2012PA05S010.pdf
https://web.stanford.edu/~jhj1/teachingdocs/Jones-on-R0.pdf
Sur la séparation des états en incubation : https://hal-pasteur.archives-ouvertes.fr/pasteur-02548181/document

Pour les initialisations des paramètres

Sur R0 particulièrement : https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-Europe-estimates-and-NPI-impact-30-03-2020.pdf
Sur R0, Tinc, TavantHosp, TavantRet : https://wwwnc.cdc.gov/eid/article/26/7/20-0282_article
https://www.infectiologie.com/fr/actualites/covid-19-nouveau-coronavirus_-n.html
Sur la durée d'inbation : https://annals.org/aim/fullarticle/2762808/incubation-period-coronavirus-disease-2019-covid-19-from-publicly-reported?searchresult=1
Sur la durée de contagion : https://www.ecdc.europa.eu/en/covid-19/questions-answers
Stats Islande (population : 360.000 habs en 2020) : https://www.covid.is/data
Sur la durée d'immunité : https://www.gov.uk/government/publications/react-2-real-time-assessment-of-community-transmission-antibody-waning/react-2-real-time-assessment-of-community-transmission-antibody-waning

Historique

Mars 2020 : Création
Avril 2020 : Séparation Etats E
Avril 2020 : Ajout exports/imports
20 octobre 2020 : Actualisation paramètres initiaux PF
04 novembre 2020 : Actualisation paramètres initiaux PF
04 novembre 2020 : Ajout de la réinfection possible
04 novembre 2020 : Ajout de la réinfection possible
23 novembre 2020 : Actualisation courbe R0 avec suite à 1.3
30 novembre 2020 : Actualisation courbe R0 avec suite optimiste à 1.15

Pour me contacter, un mail à Fabien Crépin